股指期貨與股票組合的對沖
admin
VA:股票組合的當前價值;
VF:一份期貨的當前價值(定義為期貨價格乘以期貨規模)。
如果組合是為了跟蹤股票指數,最優對沖率h*為1.0,由式(3-3)得出需要持有的期貨空頭合約數量為

當股票組合不跟蹤股指時,我們可以采用資本資產定價模型(CAPM,見本章附錄)中的β值來確定持有期貨空頭的數量。β是將組合超過無風險利率的收益與股票市場超過無風險利率的收益進行回歸所產生的最佳擬合直線的斜率。當β=1時,組合收益往往跟蹤市場收益;當β=2時,組合超過無風險利率的收益等于股票市場超過無風險收益的兩倍;當β=0.5時,組合超過無風險利率的收益等于股票市場超過無風險收益的一半,等等。
一個β值等于2.0的組合對市場的敏感度是一個β值等于1.0的組合的兩倍。因此,為了對沖這一組合,我們將需要兩倍數量的合約。類似地,一個β值等于0.5的組合對市場的敏感度是一個β值等于1.0的組合的一半,因此我們只需要一半數量的合約來對沖風險。一般來講

將式(3-5)與式(3-3)比較,可以得出
我們通過例子來說明利用這個公式做對沖時的效果很好。假定利用4個月期限的期貨合約來對組合在今后3個月內的價值進行對沖。假設
標普500股指當前值=1000
標普500股指期貨價格=1010
組合價值=5050000美元
無風險利率=每年4%
股指票息收益率=每年1%
組合的β=1.5
1份期貨合約是交割250美元乘以股指,因此,VF=250×1010=252500。由式(3-5)得出對沖組合所需要持有的空頭期貨合約數量為
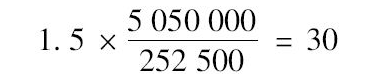
30×(1010-902)×250=810000(美元)
股指的虧損為10%。股指每年支付1%的股息收益率,或每3個月0.25%。因此,將股息考慮在內時,股指投資者在3個月里的收益為-9.75%。由于組合的β是1.5,由資本資產定價模型得出:
組合的收益期望-無風險利率=1.5×(股指收益-無風險利率)
3個月期的無風險利率大約為1%,因此,組合在3個月內的收益期望(%)為
1.0+[1.5×(-9.75-1.0)]=-15.125
因此組合在3個月后價值的期望(包括股息)為
5050000×(1-0.15125)=4286187(美元)
在考慮對沖收益后,對沖者頭寸價值的期望值為
4286187+810000=5096187(美元)
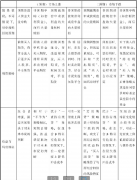
表3-4總結了這些計算,同時也對股指在到期時可能取的其他數值進行了類似的計算。我們可以看出,在3個月后,對沖者的頭寸幾乎與股指的取值無關。
表3-4 股指對沖的表現

在這個例子中,我們還沒有討論期貨價格與即期價格之間的關系。在第5章,我們將看到這里所假設的當前期貨價格1010與我們假設的利率和股息率是一致的。這一結論對于表3-4中3個月后的期貨價格也適用。