完美市場假設下的股指期貨定價模型
admin
(一)靜態持有成本模型
在眾多期貨定價模型中,持有成本模型(Cost of Carry Model)是最重要也是最基本的模型,被廣泛應用于商品期貨和金融期貨的定價實踐中。持有成本模型是Cornell & French(1983)在完美市場(Perfect Markets)假設下,基于一個套利組合而推導出來的期貨定價模型,其假設條件有:(1)資本市場是完美的,即無稅收、無交易成本,不限制賣空且資產是完全可分割的;(2)可以以無風險利率借入及貸出資金,且借、貸利率相同并為一固定常數;(3)股利的支付已知且為一固定常數,即無股利不確定風險;(4)期貨和現貨頭寸均持有到期貨合約到期日;(5)無結算風險。
持有成本是持有成本定價模型的核心。所謂持有成本,是指投資者為持有某種現貨品種直至相應的期貨合約到期時所必須支付的凈成本,即因融資購買現貨資產而支付的融資成本減去持有現貨資產而取得的收益。就金融期貨而言,持有成本是指為相關金融資產進行融資所支付的凈利息成本。
從理論上講,在股指期貨交易中,由于合約在結算日才能進行交割,因此合約的賣方在交割日前因持有相應的股票組合獲得股利的同時,也放棄了相應時間段的現金收益;而合約的買方因推遲交割在損失了相應的股利收入的同時,則可以獲得因持有現金所得到的利息收入。因此,根據無套利原理,股指期貨合約的定價應考慮買賣雙方的凈損益。基于以上原理,有以下等式成立:
股指期貨合約的價格=現貨價格+融資成本-股息收益

(4-1)
式中:
Ft:為在t時刻購買股指期貨合約的期貨價格;
St:為t時刻的股票指數;
d:為股票組合年均股息紅利收益率;
rf:為無風險收益年利率;
T:為股指期貨合約到期日。
假定投資者持有與股票指數相對應的股票組合,那么從t時刻開始到T時刻,持有成本則包含兩部分:一部分為投資于該項股票資產的機會成本,即實際借款成本;另一部分則為投資者從t時刻開始到T時刻取得的股息紅利收入。
根據持有成本模型,股指期貨的價格主要受到股票現貨指數水平St、無風險利率水平rf、股票組合股利收益率d以及合約有效期長短(T-t)等因素的影響。其中,無風險利率水平rf和股票組合股利收益率d是關鍵因素。
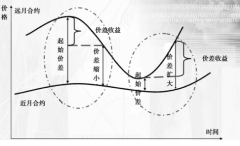
如果rf-d>0,則期貨價格大于現貨價格,稱該市場為正向持倉市場(Positive Carry Market);如果rf-d<0,則期貨價格小于現貨價格,稱該市場為反向持倉市場(Negative Carry Market)。
市場中的套利行為有助于使股指期貨價格和現貨價格保持一個穩定的差異,這個差異就是持有成本。一旦現實市場中的期貨價格與其理論價格不一致,并且超過一定的水平時,就會出現套利機會,套利者會迅速做出反應,通過無風險套利使得期貨價格與現貨價格恢復到均衡狀態。
比如,當股指期貨實際價格高于理論價格時,即Ft>S t+S t(r f-d)(T-t),投資者可以在股指期貨市場于時間t賣出股指期貨合約的同時,在股票市場買入相應的指數組合,并在時間T進行反向操作而獲得無風險收益,這稱之為正向套利策略。相反,當股指期貨實際價格低于理論價格時,即Ft<S t+S t(r f-d) (T-t),投資者可以在股指期貨市場于時間t買入股指期貨合約,同時在股票市場賣出相應的指數組合,并在時間T進行反向操作而獲得無風險收益,這稱之為反向套利策略。
(二)動態持有成本模型
以上考慮的是間斷時間下的靜態持有成本模型。如果假設時間是連續的,即期貨交易的利潤立即被繼續投資,則可將靜態模型改寫為動態持有成本模型,如式(4.2、4.3)所示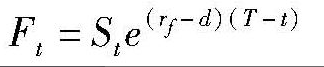
(4-2)

(4-3)
公式(4.3)表明,在持有成本等因素一定的條件下,股指現貨價格與股指期貨價格呈正向關系。此時,
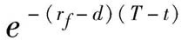
實證研究發現,股指期貨實際價格與持有成本定價模型所估算出的理論價格之間有顯著差異。Fama & French(1987)對多種標的物且期限不同的期貨合約的實證研究顯示,各合約月度基差的標準差變化范圍在1.5%~22.2%之間。Pindyck(1993)用標的資產未來現金流的現值代表便利收益,對持有成本模型進行的研究發現,期貨價格偏離其理論定價且無法用便利收益來解釋,從而認為出現偏差的原因是由于市場的不完美。Brenner、Subrahoanyam & Uno(1989)的研究認為,股指期貨理論定價和實際定價的大部分誤差無法直接由交易成本來解釋,對現貨市場的賣空限制等因素是影響誤差的最大原因。