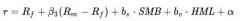在資產定價、投資組合管理學中,三因子模型指法馬-佛倫奇三因子模型,一個資本資產定價模型的改進理論。該模型的提出是基于美國股市歷史回報率的實證研究結果,目的在于解釋股票市場的平均回報率受到哪些風險溢價因素的影響。模型設計者,尤金·法馬和肯尼斯·佛倫奇曾俱在美國芝加哥大學布斯商學院供職。
模型的設定和實證分析
在資本資產定價模型(CAPM)等傳統理論下,投資組合的全部風險溢價由Beta系數表示。但是這一模型在解釋股票市場回報的現實情況上,如一月效應,遇到了諸多挑戰。法馬和佛倫奇(1992)觀察發現市值較小、市值賬面比較低的兩類公司更有可能取得優于市場水平的平均回報率。由此三因子模型通過引入二個新的解釋變量:市凈率、公司規模,與CAPM中的市場指數一同估計股票的回報水平,即:

其中 投資組合的期望收益率,
投資組合的期望收益率,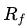 是市場無風險收益率,
是市場無風險收益率, 是市場組合的收益率,三個變量的待估系數
是市場組合的收益率,三個變量的待估系數 是市場組合風險溢價、規模溢價、市凈率溢價三個因素變化對期望收益率的影響,其中市場組合風險溢價的系數beta概念接近于CAPM模型中的beta系數,公司規模變量SMB是指由市值小的公司組成的投資組合回報與市值大的公司組成的投資組合回報之差,市凈率溢價HML是賬面價值比較高的公司組成的投資組合回報與比值較低的公司投資組合回報之差。α是超額收益率,在理想的情況下,投資組合的超額回報將全部被三因素解釋,從而α應在統計學意義上等于0.
是市場組合風險溢價、規模溢價、市凈率溢價三個因素變化對期望收益率的影響,其中市場組合風險溢價的系數beta概念接近于CAPM模型中的beta系數,公司規模變量SMB是指由市值小的公司組成的投資組合回報與市值大的公司組成的投資組合回報之差,市凈率溢價HML是賬面價值比較高的公司組成的投資組合回報與比值較低的公司投資組合回報之差。α是超額收益率,在理想的情況下,投資組合的超額回報將全部被三因素解釋,從而α應在統計學意義上等于0.
在回歸分析中,三因子的數據通過市凈率的高低、公司規模的大小,將股票市場上所有公司分成10個等市值的投資組合,并利用他們的歷史數據計算三因子各自的溢價水平。這些額數據現在仍可以從肯尼斯·弗倫奇的網站上找到。
當規模溢價、市凈率溢價確定后,其系數通過線性回歸的方式進行計算。法馬和佛倫奇的計算結果顯示約70%的收益率水平可以通過此種分組方式,經由CAPM模型計算得出;而超過90%的收益率可以通過修正后的模型,法馬-佛倫奇三因子模型得到解釋。而規模溢價、市凈率溢價的回歸系數在統計學意義上顯著,意味著三因子模型可能捕捉到了市場組合風險溢價尚不能解釋的信息。此外,規模溢價的系數為正,意味著那些市值較小的公司組成的投資組合,可以預期能帶來更高的回報,與更高的風險。
改進與衍生研究
格里芬的研究證明三因子模型是一個國別性的模型,全球經濟變量對各國股票市場的收益率水平影響不如各國內部經濟變量的影響顯著[3]。因此,一些基于各國國內股票市場的實證研究也取得了相關進展,如英國、德國、瑞士。事實上,作為套利定價理論的一個應用,經過改進的法馬-佛倫奇三因子模型還有學者用來解釋GDP增長率和債券市場收益率。
本文由東方銅牛網整理編輯,轉載 三因子模型介紹與實證分析 請注明文章地址鏈接。

 投資組合的期望收益率,
投資組合的期望收益率,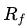 是市場無風險收益率,
是市場無風險收益率, 是市場組合的收益率,三個變量的待估系數
是市場組合的收益率,三個變量的待估系數 是市場組合風險溢價、規模溢價、市凈率溢價三個因素變化對期望收益率的影響,其中市場組合風險溢價的系數beta概念接近于CAPM模型中的beta系數,公司規模變量SMB是指由市值小的公司組成的投資組合回報與市值大的公司組成的投資組合回報之差,市凈率溢價HML是賬面價值比較高的公司組成的投資組合回報與比值較低的公司投資組合回報之差。α是超額收益率,在理想的情況下,投資組合的超額回報將全部被三因素解釋,從而α應在統計學意義上等于0.
是市場組合風險溢價、規模溢價、市凈率溢價三個因素變化對期望收益率的影響,其中市場組合風險溢價的系數beta概念接近于CAPM模型中的beta系數,公司規模變量SMB是指由市值小的公司組成的投資組合回報與市值大的公司組成的投資組合回報之差,市凈率溢價HML是賬面價值比較高的公司組成的投資組合回報與比值較低的公司投資組合回報之差。α是超額收益率,在理想的情況下,投資組合的超額回報將全部被三因素解釋,從而α應在統計學意義上等于0.